Shares

This is a very short introduction to graph theory. We will be talking about directed and undirected graphs, the formulas to find the maximum possible edges for them and the mathematical proofs that underlie the philosophy of why they work. This is my first use of LaTeX on Mr. Geek.

Graph Theory

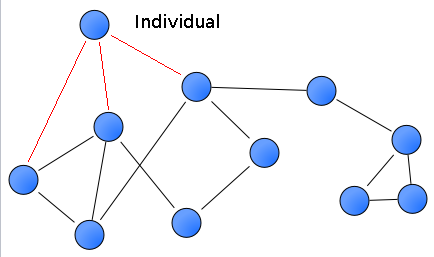
Graph theory is a branch of mathematics and computer science that is concerned with the modeling of relationships between objects. A graph is a network of vertices and edges. In an ideal example, a social network is a graph of connections between people. A vertex hereby would be a person and an edge the relationship between vertices. Here’s an example.

Directed Graphs

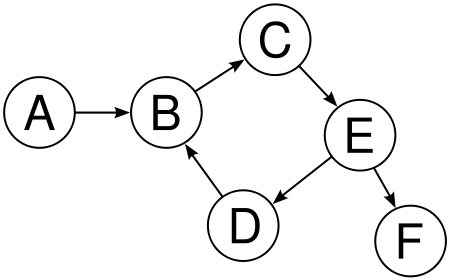
A directed graph is a graph with directions. For instance, Twitter is a directed graph. Everyone you follow doesn’t necessarily mean they follow you back. A follow can be represented as a directed edge, using an arrow. An example of a directed graph is shown below.

Maximum edges in a Directed Graph

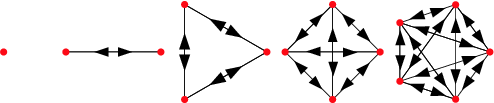
The formula for finding the maximum number of edges in a directed graph is trivial. This would happen if every vertex in the graph is connected with every other vertex, in both directions. Although not possible in a practical social network like Twitter, it is an interesting mathematical property that we can prove by mathematical induction.

\text{Let \textit {n} be the total number of vertices in a directed graph \textbf {D}, then:}

{D(n)= n(n-1)}

Wolfram (c)

\text{ Finding maximum edges when \textit {n=3} }

{D(3)= n(n-1)

{D(3)= {3(3-1) = 3(2) = 6}

\text {As you can see, the maximum edges that a 3 vertex directed graph can have are 6. }

\text {Proof by Induction: Let us prove why this works by mathematical induction.}

\textbf {Base case: \textit {assume n=k, so we set k=2 for f(k)} }

{f(2)= k(k-1) }

{f(2)= 2(2-1) = 2(1) = 2}

\text {It works for the base case, so we must prove for \textit {f(k+1).} }

\textbf {Inductive case: \textit {f(k+1)} }

\text {Our goal here is to arrive at: \textbf {f(k+1)=(k+1)(k+1-1)}}

\text { Note that we add 2k as this is the inductive step. }

{ f(k+1)= k(k-1) +2k }

{ f(k+1)= k^{2} -k +2k }

{ f(k+1)= k^{2} +k }

\text {We can write this as } \textit {f(k+1) = (k+1)(k+1-1)} }

\textbf {Because we know that:}

{ f(k+1) = (k+1)(k+1-1) = k^{2} +k-k+k+1-1 = k^{2} +k}

\text {Hence, it is proven why this equation works.}

Undirected Graphs

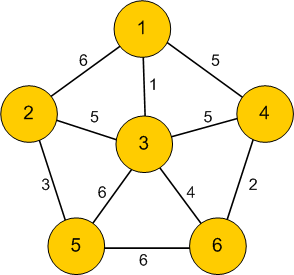
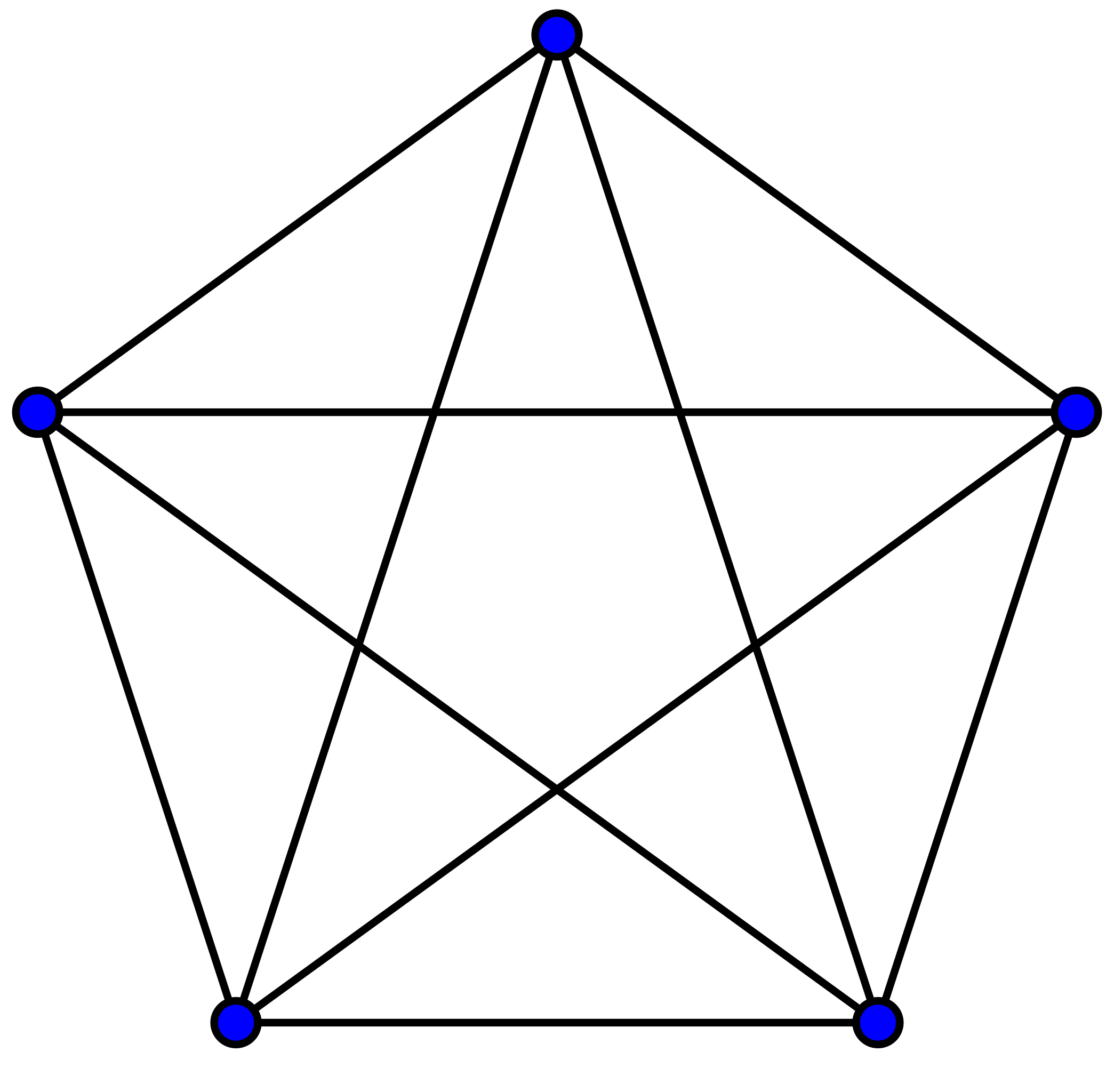
Undirected graphs are pretty interesting. Think of Facebook. Every person you add makes it a 2 way connection by default. Facebook is an undirected graph, where the edges don’t have any orientation. Here’s an image of an undirected graph. Note the lack of arrows.

 

Maximum edges in a Undirected Graph

The formula for finding the maximum number of edges in an undirected graph is trivial. This would happen if every vertex is connected with every other vertex in the graph. Imagine your core family, consisting of your brother, sister, mother and father. The graph is complete because every member (node) is connected (edge) with everyone else. Like before, we will use mathematical induction to prove why the formula works.

\text{Let \textit {n} be the total number of vertices in a undirected graph \textbf {D}, then:}

{D(n)= \frac {n(n-1)}{2} }

\text{ Finding maximum edges when \textit {n=5} }

{D(5)= \frac {n(n-1)}{2} }

{D(5)= \frac {5(5-1)}{2} = \frac {5(4)}{2} = 10}

\text {As you can see, the maximum edges that a 5 vertex undirected graph can have are 10. }

\text {Proof by Induction: Let us prove why this works by mathematical induction.}

\textbf {Base case: \textit {assume n=k, so we set k=2 for f(k)} }

{f(2)= \frac {k(k-1)}{2} }

{f(2)= \frac {2(2-1)}{2} = \frac {2(1)}{2} = 1}

\text {It works for the base case, so we must prove for \textit {f(k+1).} }

\textbf {Inductive case: \textit {f(k+1)} }

\text {Our goal here is to arrive at: } \mathbf {f(k+1)= \frac{(k+1)(k+1-1)}{2} }

\text { Note that we add k as this is the inductive step. }

{ f(k+1)= \frac {k(k-1)}{2} +k }

{ f(k+1)= \frac {k(k-1)}{2} +\frac {2k}{2} }

{ f(k+1)= \frac {k(k-1)+2k}{2} }

{ f(k+1)= \frac {k^{2} -k +2k}{2} }

{ f(k+1)= \frac {k^{2} +k}{2} }

\text {We can write this as } \mathit {f(k+1) = \frac {(k+1)(k+1-1)}{2}} }

\textbf {Because we know that:}

{ f(k+1) = \frac {(k+1)(k+1-1)}{2} = \frac {k^{2} +k-k+k+1-1}{2} = \frac {k^{2} +k}{2} }

\text {Hence, it is proven why this equation works.}

About Ali Gajani

Hi. I am Ali Gajani. I started Mr. Geek in early 2012 as a result of my growing enthusiasm and passion for technology. I love sharing my knowledge and helping out the community by creating useful, engaging and compelling content. If you want to write for Mr. Geek, just PM me on my Facebook profile.